SYMROBOTICS

SymRobotics
A Sym2Code add-on to design and implement highly complex robotics systems using the Object Oriented Programming capabilities of MATLAB®.
Robots are designed and combined together as objects.
Classical results from direct kinematics, differential kinematics and lagrangian dynamics can be obtained easily as numerical results or symbolic function, providing an elegant and simple method to generate code using Sym2Code.
Basic Objects
- Rotational Joints
- Linear Joints
- Roto-Translations
Each part of the SymRobot can be identified with a Label, to have access to its internal state given by position and orientation.
The SymRobot can be built sequentially using the Tip point which is automatically assigned to the last element added into the sequence.
The Tip can be reset to allow user to insert different object into the same point (i.e. adding more fingers into a hand).
symbolic ready
All the calculation involving a SymRobot object can be performed using numerical or symbolic variables.
Automatic generation of the joint variables make use of the Labels to allow easy and practical naming.
Finger object
classdef RobotModelFinger < SymRobot
%----------------------------------------------------------------------
% Filename: RobotModelFinger.m
% Class: RobotModelFinger
% Fcn:
%
% Description: Finger Model
%
% Author: Vincenzo Calabro' <vincenzo@cybertronics.cloud>
% Copyright: Cybertronics AS 2016-2018.
%----------------------------------------------------------------------
properties (Access = private)
aLength
end
methods
function oFinger = RobotModelFinger(aL, szLabel)
narginchk(2,2);
nargoutchk(0,1);
assert(~isempty(aL));
assert(~isempty(szLabel));
assert(ischar(szLabel));
if isa(aL,'sym')
dPi_2 = sym(pi/2);
else
dPi_2 = pi/2;
end
oFinger = oFinger@SymRobot(szLabel);
oFinger.AddToTip(SymRobotNodeJointRot(0.0,sprintf('%s_A0',szLabel)));
oFinger.AddToTip(SymRobotNodeRotoTranslation(LibMath.RotX(-dPi_2), [0;0;0]));
for i=1:numel(aL)
oFinger.AddToTip(SymRobotNodeJointRot(0.0,sprintf('%s_A%d',szLabel,i)));
oFinger.AddToTip(SymRobotNodeRotoTranslation(eye(3), [aL(i);0;0]));
end
oFinger.AddToTip(SymRobotNodeRotoTranslation(LibMath.RotX(dPi_2), [0;0;0]));
oFinger.AddToTip(SymRobotNodeRotoTranslation(eye(3), [0;0;0],sprintf('%s_Tip',szLabel)));
oFinger.aLength = aL;
end
end
end
DIRECT KINEMATICS
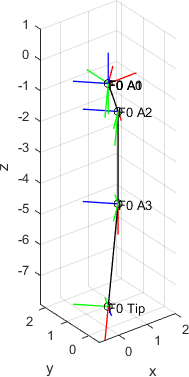
function Example_KinematicsFingerNumeric()
clc
F = RobotModelFinger([3, 3, 3], 'F0');
q = F.GetJointStruct();
fprintf('The Robotic Finger has the following objects:\n');
disp(F);
fprintf('Available Joints for Robotic Finger:\n');
disp(q);
q.F0_A0=pi/4;
q.F0_A1=pi/4;
q.F0_A2=pi/4;
q.F0_A3=pi/4;
% Update the Kinematic States
F.DirectKinematics(q);
% Get State of the joint F0_A2
szNode = 'F0_A2';
fprintf('Getting info of the node %s...\n',szNode);
fprintf('\nNode %s contains the following childs:\n',szNode);
oNode = F.GetNode(szNode); disp(oNode);
fprintf('\nNode %s has the following state:\n', szNode);
oState = GetState(oNode); disp(oState);
fprintf('\nState of %s is composed of:\n', szNode);
fprintf('Position:\n');
p = GetPosition(oState); disp(p);
fprintf('Attitude (DCM):\n');
R = GetRotation(oState); disp(R);
% u for unnamed nodes
% j for joints
% a for all (u,j)
% l for links
plot(F, 'ujalt')
end
SYMBOLIC KINEMATICS
function Example_KinematicsFingerSymbolic()
clc
syms L1 L2 L3 real
L = [L1;L2;L3];
F = RobotModelFinger(L, 'F0');
q = F.GetJointSymVariables();
fprintf('The Robotic Finger has the following objects:\n');
disp(F);
fprintf('Available Joints for Robotic Finger:\n');
disp(q);
% Update the Kinematic States
F.DirectKinematics(F.SetJointInput(q));
% Get State of the End Effector
szNode = 'F0_Tip';
fprintf('Getting info of the node %s...\n', szNode)
oNode = F.GetNode(szNode);
oState = GetState(oNode);
fprintf('\nSymbolic Position:\n');
p = GetPosition(oState)
fprintf('\nSymbolic Attitude (DCM):\n');
R = GetRotation(oState)
end
DIFFERENTIAL KINEMATICS
function Example_DifferentialKinematicsFingerNumeric()
clc
syms L1 L2 L3 real
L = [L1;L2;L3];
F = RobotModelFinger(L, 'F0');
q = F.GetJointSymVariables();
fprintf('The Robotic Finger has the following objects:\n');
disp(F);
fprintf('Available Joints for Robotic Finger:\n');
disp(q);
% Update the Kinematic States
F.DirectKinematics(F.SetJointInput(q));
% Get State of the finger tip
oTip0 = F.GetNode('F0_Tip');
Je = oTip0.DifferentialKinematics(F.SetJointInput(q))
end
COMBINING FINGERS INTO HAND
...
oHand = oHand@SymRobot(szLabel);
oHand.AddToTip(SymRobotNodeRotoTranslation(LibMath.RotX(-dPi_2), [0;0;0]));
oHand.AddToTip(SymRobotNodeJointRot(dZero,sprintf('%s_R0',szLabel)));
oHand.AddToTip(SymRobotNodeRotoTranslation(LibMath.RotX(dPi_2), [0;0;0],'BaseHand'));
oHand.AddToTip(SymRobotNodeRotoTranslation(eye(3), L(:,1)));
oHand.AddToTip(RobotModelFinger(S(:,1),sprintf('%s_F5',szLabel)));
oHand.SetTip('BaseHand');
oHand.AddToTip(SymRobotNodeRotoTranslation(eye(3), L(:,2)));
oHand.AddToTip(RobotModelFinger(S(:,2),sprintf('%s_F4',szLabel)));
oHand.SetTip('BaseHand');
...
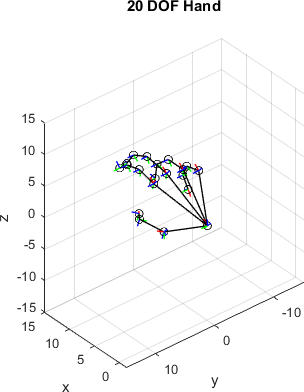
function Example_KinematicsHandNumeric()
H = RobotModelHand('HL');
q = H.GetJointStruct();
N = 10;
fprintf('Hand has %d DoF\n',numel(fieldnames(q)))
for t=0:1/N:1-1/N
q.HL_R0=-pi/4*t;
q.HL_F5_A0=0;
q.HL_F5_A1=pi/3*t;
q.HL_F5_A2=pi/3*t;
q.HL_F5_A3=pi/3*t;
q.HL_F4_A0=0;
q.HL_F4_A1=pi/4*t;
q.HL_F4_A2=pi/4*t;
q.HL_F4_A3=pi/4*t;
q.HL_F3_A0=0;
q.HL_F3_A1=pi/5*t;
q.HL_F3_A2=pi/5*t;
q.HL_F3_A3=pi/5*t;
q.HL_F2_A0=0;
q.HL_F2_A1=pi/6*t;
q.HL_F2_A2=pi/6*t;
q.HL_F2_A3=pi/6*t;
q.HL_F1_A0=0;
q.HL_F1_A1=pi/3*t;
q.HL_F1_A2=pi/3*t;
H.DirectKinematics(q);
plot(H,'la');
xlim(15*[-0.1,1])
ylim(15*[-1,1])
zlim(15*[-1,1])
view(-130,35)
title(sprintf('%d DOF Hand\n',numel(fieldnames(q))))
drawnow
end
end
LAGRANGIAN DYNAMICS

q =
\begin{pmatrix}
q_x \\ q_\psi
\end{pmatrix}
\ddot{q} = B^{-1}(q) \left( -C(q,\dot{q})\dot{q} -g(q) + \tau \right)
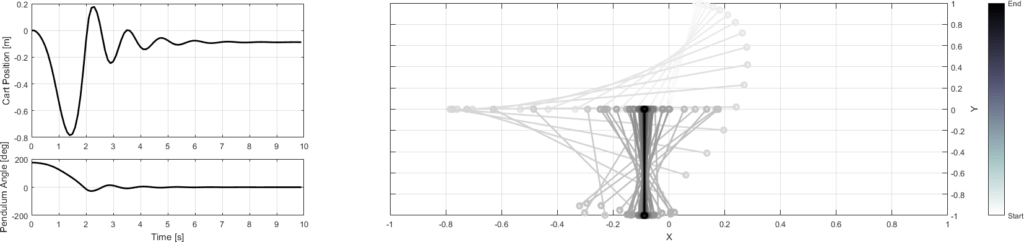
function PendulumOnCartDynamicalModel()
dPi_2 = sym(pi/2);
% Pendulum Length
syms dL real
oPendulum = SymRobot('PendulumOnCart');
oPendulum.AddToTip(SymRobotNodeRotoTranslation(LibMath.RotY(dPi_2), [0;0;0]));
% Linear Displacement of the CART is a Linear Joint
oPendulum.AddToTip(SymRobotNodeJointLin(0.0, 'X'));
% Add a Label for the CART
oPendulum.AddToTip(SymRobotNodeRotoTranslation(LibMath.RotY(-dPi_2), [0;0;0],'CART'));
oPendulum.AddToTip(SymRobotNodeRotoTranslation(LibMath.RotX(dPi_2), [0;0;0]));
oPendulum.AddToTip(SymRobotNodeRotoTranslation(LibMath.RotZ(-dPi_2), [0;0;0]));
% Angular Displacement of the MASS is a Rotational Joint
oPendulum.AddToTip(SymRobotNodeJointRot(0.0, 'PSI'));
% Add a Label for the CART
oPendulum.AddToTip(SymRobotNodeRotoTranslation(eye(3), [dL;0;0], 'TIP'));
% Joint states and derivatives
sQ = oPendulum.GetJointSymVariables('q');
sQdot = oPendulum.GetJointSymVariables('q_dot');
sQddot = oPendulum.GetJointSymVariables('q_ddot');
% Masses of the components: M is CART, m is TIP
% Gravity and direction
syms M m g0 real
gn = [0;0;-1]*g0;
oCart = oPendulum.GetNode('CART');
oTip = oPendulum.GetNode('TIP');
% Compute the Lagrangian function: T-U as the difference between
% Kinetic and Potential Energy
Lagrangian = simplify(...
oCart.Lagrangian(sQ, sQdot, M, zeros(3), gn) + ...
oTip.Lagrangian(sQ, sQdot, m, zeros(3), gn));
% Get the Dynamical Model:
% sQddot = B^-1*(-C*sQdot-g);
[B, C, g, ~] = SymRobot.LagrangianModel(sQ, sQdot, sQddot, Lagrangian)
end
Example of simulation of the generated model with additional viscous drag:
\tau = -D \dot{q}