CYBERTRONICS

Advanced Cybernetics Solutions

SYM2CODE
SYMROBOTICS
ABOUT US

sym2code knowledge base

Sym2Code Example

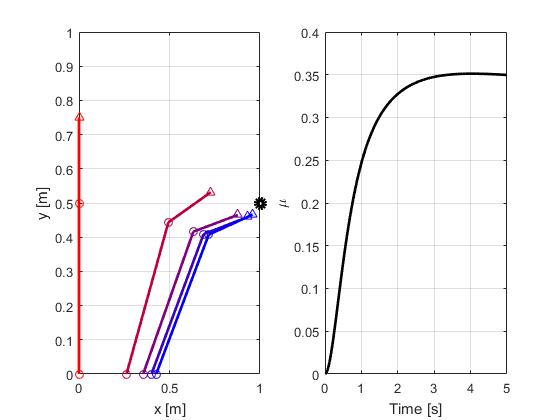
Check the control design via simulation before to deploy the final code.

Control Law Design

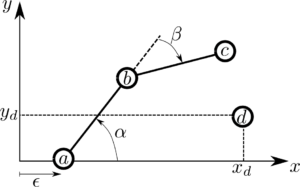
Let us consider the system depicted in picture.
The position of the three points of interest can be easily found as:
p_a = \begin{pmatrix} \epsilon \\ 0\end{pmatrix}
p_b = p_a + R_\alpha \begin{pmatrix} l_1 \\ 0\end{pmatrix}, \qquad R_\alpha = \begin{pmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix}
p_c = p_b + R_\alpha R_\beta \begin{pmatrix} l_2 \\ 0\end{pmatrix}, \qquad R_\beta = \begin{pmatrix} \cos \beta & -\sin \beta \\ \sin \beta & \cos \beta \end{pmatrix}
Considering the joint variables:
q = \begin{pmatrix} \epsilon, & \alpha, & \beta \end{pmatrix}^\top
we can formulate the control problem of finding the control law to reduce asymptotically the error:
\tilde{p} = p_d – p_c(q)
between a fixed position p_d \in \mathbb{R}^2 such that \dot{p}_d = 0 and the result of the direct kinematics represented by the function p_c(q): \mathbb{R}^3 \rightarrow \mathbb{R}^2.
Let us consider a Lyapunov function:
V(\tilde{p}) = \frac{1}{2} \tilde{p}^\top \tilde{p} \succ 0 \quad \forall \quad \tilde{p} \neq 0
computing the time derivative we obtain:
\dot{V}(\tilde{p}) = \tilde{p}^\top (-J(q)\dot{q}), \qquad J(q) =\frac{\partial p_c(q)}{\partial q}
where J(q) is the analytical Jacobian.
As the choice of the control action should enforce negative definiteness for the Lyapunov function time derivative, a possible choice can be immediately identified by: \dot{q} = K J^\top(q) \left( p_d – p_c(q) \right)
It is well known that kinematics singularities might affect the control results as the matrix J(q) K J^\top(q) is responsible of the quadratic form: \dot{V}(\tilde{p}) = -\tilde{p}^\top J(q) K J^\top(q) \tilde{p} \prec 0
A good indicator of the singularity proximity is given by the manipulability computed as: \mu =det(J(q)J^\top(q))

Let us now convert our math results into runnable code with Sym2Code

Code Generation

% Joint variables
q = SymVectorCol('q',{'epsilon','alpha','beta'}, 'Joint State');

% Arms length
L = SymVectorCol('l',1:2, 'Link Length');

% Rotation matrices
R_alpha = [cos(q(2)), -sin(q(2)); sin(q(2)), cos(q(2))];
R_beta = [cos(q(3)), -sin(q(3)); sin(q(3)), cos(q(3))];

% Direct kinematics of the points of interest
p_a = Sym('p_a',[q(1);0],'Position A');
p_b = Sym('p_b',p_a + R_alpha*[L(1);0],'Position B');
p_c = Sym('p_c',simplify(p_b + R_alpha*R_beta*[L(2);0]),'Position C');

Sym2Code({p_a, p_b, p_c}, 'PRRKine', {q, L});

% Lyapunov control law
p_d = SymVectorCol('p_d',{'x','y'}, 'Desired Position');
K = SymVectorCol('K',{'x','alpha', 'beta'}, 'Gain');
J = Sym('J', simplify(jacobian(p_c,q)), 'Analytic Jacobian');
q_dot_c = Sym('u', simplify(diag(K)*J'*(p_d-p_c)), 'Kinematic Control');

Sym2Code({q_dot_c, J}, 'PRRCtrl', {q, L, p_d, K});

Resulting Code

Simulating System


% Time and number of samples
Ts  = 0.01;
Tf  = 5.0;
t   = 0:Ts:Tf;
N   = numel(t);

% Joint state, manipulability index and points of interest
q   = zeros(3,N);
mu  = zeros(1,N);
p_a = zeros(2,N);
p_b = zeros(2,N);
p_c = zeros(2,N);

% Initial condition: vertical position
q(:,1) = [0.0; pi/2; 0];

% Arms length
L      = [0.5; 0.25];

% Gain and desired position
K      = [0.4; 1.0; 5.0];
p_d    = [1;0.5];

% Simulate kinematics control
figure(1);
subplot(1,2,1)
plot(p_d(1),p_d(2), 'ok', 'LineWidth',4), hold on;
for k=1:N
    
    % Compute the location of the points of interest
    [p_a(:,k), p_b(:,k), p_c(:,k)] = PRRKine(q(:,k), L);
    
    % Compute control action
    [q_dot_c, J] = PRRCtrl(q(:,k), L, p_d, K);
    
    % Evaluate the manipulability index
    mu(k) = det(J*J');
    
    % Plot trajectory: red to blue over time
    if k==1 || mod(k,floor(N/4))==0
        Color = [1;0;0]*(N-k)/N + [0;0;1]*(k/N);
        % Plot the three points
        plot(p_a(1,k),p_a(2,k),'o','Color',Color), hold on;
        plot(p_b(1,k),p_b(2,k),'o','Color',Color)
        plot(p_c(1,k),p_c(2,k),'^','Color',Color)
        
        % Plot the two links
        plot([p_a(1,k),p_b(1,k)],...
            [p_a(2,k),p_b(2,k)],'-', 'LineWidth',2,'Color',Color);
        plot([p_b(1,k),p_c(1,k)],...
            [p_b(2,k),p_c(2,k)],'-', 'LineWidth',2,'Color',Color);
    end
    
    % Integrate with forward Euler
    q(:,k+1) = q(:,k) + Ts*q_dot_c;
end
grid on, hold off;
xlim([0,1]); ylim([0,1])
xlabel('x [m]'), ylabel('y [m]');

% Plot manipulability index over time
subplot(1,2,2)
plot(t, mu, 'k', 'LineWidth',2);
grid on; hold off;
xlim([0,Tf]),
xlabel('Time [s]'), ylabel('\mu')

Get in Touch

By continuing to use the site, you agree to the use of cookies. more information

The cookie settings on this website are set to "allow cookies" to give you the best browsing experience possible. If you continue to use this website without changing your cookie settings or you click "Accept" below then you are consenting to this.

Close