sym2code knowledge base
Sym2Code Example
Speed Projection using Roll Pitch Yaw
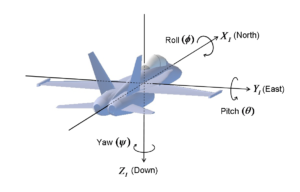
Let us consider the attitude of a body through a classic Euler angle representation, using roll, pitch and yaw angles \Theta = \begin{pmatrix}\phi,\theta,\psi\end{pmatrix}^T \in \mathbb{R}^3:
R^n_b(\Theta) =
\begin{pmatrix}
\cos(\psi) &-\sin(\psi) &0\\
\sin(\psi) &\cos(\psi) &0\\
0 &0 &1
\end{pmatrix}
\begin{pmatrix}
\cos(\theta) &0, &\sin(\theta)\\
0 &1 &0\\
-\sin(\theta) &0, &\cos(\theta)
\end{pmatrix}
\begin{pmatrix}
1 &0 &0\\
0 &\cos(\phi) &-\sin(\phi)\\
0 &\sin(\phi) &\cos(\phi)
\end{pmatrix}
The body speed with surge sway and heave components v^b = \begin{pmatrix} u, v, w\end{pmatrix}^T \in \mathbb{R}^3 can be projected into the navigation frame as follows:
v^n = R^n_b(\Theta) v^b
Let us now create a piece of code to automatically compute the rotation matrix R^n_b and the navigation speed v^n.
% Roll Pitch Yaw Angles
syms roll pitch yaw q real
% Direction Cosine Matrices
Rx = [ 1, 0 0;
0, cos(roll), -sin(roll);
0, sin(roll), cos(roll)];
Ry = [ cos(pitch), 0, sin(pitch);
0, 1, 0;
-sin(pitch), 0, cos(pitch)];
Rz = [ cos(yaw), -sin(yaw), 0;
sin(yaw), cos(yaw) , 0;
0, 0, 1 ];
% Input Parameterization
RPY= Sym('RPY',[roll; pitch; yaw],'Roll Pitch Yaw');
Vb = SymVectorCol('Vb',{'surge','sway','heave'}, 'Body Speed');
% Output Variables
Rnb= Sym('Rnb',simplify(Rz*Ry*Rx),'Attitude');
Vn = Sym('Vn',simplify(Rnb*Vb),'Navigation Speed');
% Generate Code!
Sym2Code({Vn, Rnb}, 'SpeedMap', {RPY, Vb});
Regular Code
function [Vn,Rnb, bError] = SpeedMap(RPY,Vb)
%-----------------------------------------------------------------------------
% This code has been automatically generated using Sym2Code Toolbox
% Sym2Code M Target
%-----------------------------------------------------------------------------
% WARNING: Modifying the following code is not recommended.
%-----------------------------------------------------------------------------
% For more information:
% - visit our webpage www.cybertronics.cloud
% - write an email to sym2code@cybertronics.cloud
%-----------------------------------------------------------------------------
% Inputs:
% RPY is a 3x1: Roll Pitch Yaw */
% Vb is a 3x1: Body Speed */
% Output:
% Vn is a 3x1: Navigation Speed */
% Rnb is a 3x3: Attitude */
%-----------------------------------------------------------------------------
% The module is named SpeedMap and has 2 inputs and 2 outputs
Vn = zeros(3,1); % Output n. 1 is: Navigation Speed
Rnb = zeros(3,3); % Output n. 2 is: Attitude
bError = true;
% Check input data
% Input n. 1 is: Roll Pitch Yaw
if(isempty(RPY)), return; end
if(size(RPY,1)~=3), return; end
if(size(RPY,2)~=1), return; end
if(~isempty(RPY(isnan(RPY)==1))), return; end
% Input n. 2 is: Body Speed
if(isempty(Vb)), return; end
if(size(Vb,1)~=3), return; end
if(size(Vb,2)~=1), return; end
if(~isempty(Vb(isnan(Vb)==1))), return; end
% Perform main calculation
% Generating optimal output for Vn which is Vn with comment: Navigation Speed
% as Vb_heave*(sin(roll)*sin(yaw) + cos(roll)*cos(yaw)*sin(pitch)) - Vb_sway*(cos(roll)*sin(yaw) - cos(yaw)*sin(pitch)*sin(roll)) + Vb_surge*cos(pitch)*cos(yaw)
Vn(1,1) = (((Vb(3,1)*((sin(RPY(1,1))*sin(RPY(3,1)))+((cos(RPY(1,1))*cos(RPY(3,1)))*sin(RPY(2,1)))))-(Vb(2,1)*((cos(RPY(1,1))*sin(RPY(3,1)))-((cos(RPY(3,1))*sin(RPY(2,1)))*sin(RPY(1,1))))))+((Vb(1,1)*cos(RPY(2,1)))*cos(RPY(3,1))));
% as Vb_sway*(cos(roll)*cos(yaw) + sin(pitch)*sin(roll)*sin(yaw)) - Vb_heave*(cos(yaw)*sin(roll) - cos(roll)*sin(pitch)*sin(yaw)) + Vb_surge*cos(pitch)*sin(yaw)
Vn(2,1) = (((Vb(2,1)*((cos(RPY(1,1))*cos(RPY(3,1)))+((sin(RPY(2,1))*sin(RPY(1,1)))*sin(RPY(3,1)))))-(Vb(3,1)*((cos(RPY(3,1))*sin(RPY(1,1)))-((cos(RPY(1,1))*sin(RPY(2,1)))*sin(RPY(3,1))))))+((Vb(1,1)*cos(RPY(2,1)))*sin(RPY(3,1))));
% as Vb_heave*cos(pitch)*cos(roll) - Vb_surge*sin(pitch) + Vb_sway*cos(pitch)*sin(roll)
Vn(3,1) = ((((Vb(3,1)*cos(RPY(2,1)))*cos(RPY(1,1)))-(Vb(1,1)*sin(RPY(2,1))))+((Vb(2,1)*cos(RPY(2,1)))*sin(RPY(1,1))));
% Generating optimal output for Rnb which is Rnb with comment: Attitude
% as cos(pitch)*cos(yaw)
Rnb(1,1) = (cos(RPY(2,1))*cos(RPY(3,1)));
% as cos(yaw)*sin(pitch)*sin(roll) - cos(roll)*sin(yaw)
Rnb(1,2) = (((cos(RPY(3,1))*sin(RPY(2,1)))*sin(RPY(1,1)))-(cos(RPY(1,1))*sin(RPY(3,1))));
% as sin(roll)*sin(yaw) + cos(roll)*cos(yaw)*sin(pitch)
Rnb(1,3) = ((sin(RPY(1,1))*sin(RPY(3,1)))+((cos(RPY(1,1))*cos(RPY(3,1)))*sin(RPY(2,1))));
% as cos(pitch)*sin(yaw)
Rnb(2,1) = (cos(RPY(2,1))*sin(RPY(3,1)));
% as cos(roll)*cos(yaw) + sin(pitch)*sin(roll)*sin(yaw)
Rnb(2,2) = ((cos(RPY(1,1))*cos(RPY(3,1)))+((sin(RPY(2,1))*sin(RPY(1,1)))*sin(RPY(3,1))));
% as cos(roll)*sin(pitch)*sin(yaw) - cos(yaw)*sin(roll)
Rnb(2,3) = (((cos(RPY(1,1))*sin(RPY(2,1)))*sin(RPY(3,1)))-(cos(RPY(3,1))*sin(RPY(1,1))));
% as -sin(pitch)
Rnb(3,1) = (-sin(RPY(2,1)));
% as cos(pitch)*sin(roll)
Rnb(3,2) = (cos(RPY(2,1))*sin(RPY(1,1)));
% as cos(pitch)*cos(roll)
Rnb(3,3) = (cos(RPY(2,1))*cos(RPY(1,1)));
% Return a valid state
bError = false;
end
Optimized Code
function [Vn,Rnb, bError] = SpeedMap(RPY,Vb)
%-----------------------------------------------------------------------------
% This code has been automatically generated using Sym2Code Toolbox
% Sym2Code M Target
%-----------------------------------------------------------------------------
% WARNING: Modifying the following code is not recommended.
%-----------------------------------------------------------------------------
% For more information:
% - visit our webpage www.cybertronics.cloud
% - write an email to sym2code@cybertronics.cloud
%-----------------------------------------------------------------------------
% Inputs:
% RPY is a 3x1: Roll Pitch Yaw */
% Vb is a 3x1: Body Speed */
% Output:
% Vn is a 3x1: Navigation Speed */
% Rnb is a 3x3: Attitude */
%-----------------------------------------------------------------------------
% The module is named SpeedMap and has 2 inputs and 2 outputs
Vn = zeros(3,1); % Output n. 1 is: Navigation Speed
Rnb = zeros(3,3); % Output n. 2 is: Attitude
bError = true;
XTmp = zeros(1,41); % Optimal Transition Variables
% Check input data
% Input n. 1 is: Roll Pitch Yaw
if(isempty(RPY)), return; end
if(size(RPY,1)~=3), return; end
if(size(RPY,2)~=1), return; end
if(~isempty(RPY(isnan(RPY)==1))), return; end
% Input n. 2 is: Body Speed
if(isempty(Vb)), return; end
if(size(Vb,1)~=3), return; end
if(size(Vb,2)~=1), return; end
if(~isempty(Vb(isnan(Vb)==1))), return; end
% Perform main calculation
% Computing sin(roll) as
XTmp(1) = sin(RPY(1,1));
% Computing sin(yaw) as
XTmp(2) = sin(RPY(3,1));
% Computing sin(roll)*sin(yaw) as
XTmp(3) = (XTmp(1)*XTmp(2));
% Computing cos(roll) as
XTmp(4) = cos(RPY(1,1));
% Computing cos(yaw) as
XTmp(5) = cos(RPY(3,1));
% Computing sin(pitch) as
XTmp(6) = sin(RPY(2,1));
% Computing cos(roll)*cos(yaw)*sin(pitch) as
XTmp(7) = ((XTmp(4)*XTmp(5))*XTmp(6));
% Computing sin(roll)*sin(yaw) + cos(roll)*cos(yaw)*sin(pitch) as
XTmp(8) = (XTmp(3)+XTmp(7));
% Computing Vb_heave*(sin(roll)*sin(yaw) + cos(roll)*cos(yaw)*sin(pitch)) as
XTmp(9) = (Vb(3,1)*XTmp(8));
% Computing cos(roll)*sin(yaw) as
XTmp(10) = (XTmp(2)*XTmp(4));
% Computing -cos(yaw)*sin(pitch)*sin(roll) as
XTmp(11) = (((-XTmp(1))*XTmp(5))*XTmp(6));
% Computing cos(roll)*sin(yaw) - cos(yaw)*sin(pitch)*sin(roll) as
XTmp(12) = (XTmp(10)+XTmp(11));
% Computing -Vb_sway*(cos(roll)*sin(yaw) - cos(yaw)*sin(pitch)*sin(roll)) as
XTmp(13) = ((-Vb(2,1))*XTmp(12));
% Computing cos(pitch) as
XTmp(14) = cos(RPY(2,1));
% Computing Vb_surge*cos(pitch)*cos(yaw) as
XTmp(15) = ((Vb(1,1)*XTmp(5))*XTmp(14));
% Computing Vb_heave*(sin(roll)*sin(yaw) + cos(roll)*cos(yaw)*sin(pitch)) - Vb_sway*(cos(roll)*sin(yaw) - cos(yaw)*sin(pitch)*sin(roll)) + Vb_surge*cos(pitch)*cos(yaw) as
XTmp(16) = ((XTmp(9)+XTmp(13))+XTmp(15));
% Computing cos(roll)*cos(yaw) as
XTmp(17) = (XTmp(4)*XTmp(5));
% Computing sin(pitch)*sin(roll)*sin(yaw) as
XTmp(18) = (XTmp(3)*XTmp(6));
% Computing cos(roll)*cos(yaw) + sin(pitch)*sin(roll)*sin(yaw) as
XTmp(19) = (XTmp(17)+XTmp(18));
% Computing Vb_sway*(cos(roll)*cos(yaw) + sin(pitch)*sin(roll)*sin(yaw)) as
XTmp(20) = (Vb(2,1)*XTmp(19));
% Computing cos(yaw)*sin(roll) as
XTmp(21) = (XTmp(1)*XTmp(5));
% Computing -cos(roll)*sin(pitch)*sin(yaw) as
XTmp(22) = ((-XTmp(6))*XTmp(10));
% Computing cos(yaw)*sin(roll) - cos(roll)*sin(pitch)*sin(yaw) as
XTmp(23) = (XTmp(21)+XTmp(22));
% Computing -Vb_heave*(cos(yaw)*sin(roll) - cos(roll)*sin(pitch)*sin(yaw)) as
XTmp(24) = ((-Vb(3,1))*XTmp(23));
% Computing Vb_surge*cos(pitch)*sin(yaw) as
XTmp(25) = ((Vb(1,1)*XTmp(2))*XTmp(14));
% Computing Vb_sway*(cos(roll)*cos(yaw) + sin(pitch)*sin(roll)*sin(yaw)) - Vb_heave*(cos(yaw)*sin(roll) - cos(roll)*sin(pitch)*sin(yaw)) + Vb_surge*cos(pitch)*sin(yaw) as
XTmp(26) = ((XTmp(20)+XTmp(24))+XTmp(25));
% Computing Vb_heave*cos(pitch)*cos(roll) as
XTmp(27) = ((Vb(3,1)*XTmp(4))*XTmp(14));
% Computing Vb_sway*cos(pitch)*sin(roll) as
XTmp(28) = ((Vb(2,1)*XTmp(1))*XTmp(14));
% Computing -Vb_surge*sin(pitch) as
XTmp(29) = ((-Vb(1,1))*XTmp(6));
% Computing Vb_heave*cos(pitch)*cos(roll) - Vb_surge*sin(pitch) + Vb_sway*cos(pitch)*sin(roll) as
XTmp(30) = ((XTmp(27)+XTmp(28))+XTmp(29));
% Computing cos(pitch)*cos(yaw) as
XTmp(31) = (XTmp(5)*XTmp(14));
% Computing cos(yaw)*sin(pitch)*sin(roll) as
XTmp(32) = (XTmp(6)*XTmp(21));
% Computing -cos(roll)*sin(yaw) as
XTmp(33) = (-XTmp(10));
% Computing cos(yaw)*sin(pitch)*sin(roll) - cos(roll)*sin(yaw) as
XTmp(34) = (XTmp(32)+XTmp(33));
% Computing cos(pitch)*sin(yaw) as
XTmp(35) = (XTmp(2)*XTmp(14));
% Computing cos(roll)*sin(pitch)*sin(yaw) as
XTmp(36) = (XTmp(6)*XTmp(10));
% Computing -cos(yaw)*sin(roll) as
XTmp(37) = (-XTmp(21));
% Computing cos(roll)*sin(pitch)*sin(yaw) - cos(yaw)*sin(roll) as
XTmp(38) = (XTmp(36)+XTmp(37));
% Computing -sin(pitch) as
XTmp(39) = (-XTmp(6));
% Computing cos(pitch)*sin(roll) as
XTmp(40) = (XTmp(1)*XTmp(14));
% Computing cos(pitch)*cos(roll) as
XTmp(41) = (XTmp(4)*XTmp(14));
% Generating optimal output for Vn which is Vn with comment: Navigation Speed
% as Vb_heave*(sin(roll)*sin(yaw) + cos(roll)*cos(yaw)*sin(pitch)) - Vb_sway*(cos(roll)*sin(yaw) - cos(yaw)*sin(pitch)*sin(roll)) + Vb_surge*cos(pitch)*cos(yaw)
Vn(1,1) = XTmp(16);
% as Vb_sway*(cos(roll)*cos(yaw) + sin(pitch)*sin(roll)*sin(yaw)) - Vb_heave*(cos(yaw)*sin(roll) - cos(roll)*sin(pitch)*sin(yaw)) + Vb_surge*cos(pitch)*sin(yaw)
Vn(2,1) = XTmp(26);
% as Vb_heave*cos(pitch)*cos(roll) - Vb_surge*sin(pitch) + Vb_sway*cos(pitch)*sin(roll)
Vn(3,1) = XTmp(30);
% Generating optimal output for Rnb which is Rnb with comment: Attitude
% as cos(pitch)*cos(yaw)
Rnb(1,1) = XTmp(31);
% as cos(yaw)*sin(pitch)*sin(roll) - cos(roll)*sin(yaw)
Rnb(1,2) = XTmp(34);
% as sin(roll)*sin(yaw) + cos(roll)*cos(yaw)*sin(pitch)
Rnb(1,3) = XTmp(8);
% as cos(pitch)*sin(yaw)
Rnb(2,1) = XTmp(35);
% as cos(roll)*cos(yaw) + sin(pitch)*sin(roll)*sin(yaw)
Rnb(2,2) = XTmp(19);
% as cos(roll)*sin(pitch)*sin(yaw) - cos(yaw)*sin(roll)
Rnb(2,3) = XTmp(38);
% as -sin(pitch)
Rnb(3,1) = XTmp(39);
% as cos(pitch)*sin(roll)
Rnb(3,2) = XTmp(40);
% as cos(pitch)*cos(roll)
Rnb(3,3) = XTmp(41);
% Return a valid state
bError = false;
end


